Fun Sudoku Tutorial
|
Sudoku puzzles are a type of Latin Square - any character cannot appear more than once in each row or column, with an extra constraint that that character also cannot appear more than once in each 3x3 cell area. In total, there are 27 such domains in a regular Sudoku puzzle. The puzzles that you find almost everywhere, including in the Soduku section of this site have numbers, although there is a version of each day's puzzle that has alternative numbers in it so that you do not have a sign that you can readily recognise unless you can read Gurmukhi numbers. In this section, there are some fun variants of the regular Sudoku puzzle - the 'normal' puzzle being the 'Wordoku' which uses a nine-letter word instead of numbers. Where letters are used instead of numbers, the letters are displayed next to the puzzle. All of the other puzzles, such as the one on the right, use more than the 27 domains (nine columns, nine rows and 9 3x3 squares of the regular Sudoku, they have one or four extra domains. The additional domains work in the same way as the usual 27 insofar as they have all nine characters in them and they cannot have any of them appearing more than once.
So, how do these extra domains work? On the right, you can see one of the Day Of the Week puzzles 'DOW-doku'. This is for Thursday so there is a lowercase 't' in only nine picture elements. The regular 27 domains work as normal but there is the 28th domain in the form of the 't'. This extends across five of the 3x3 domains as well as four columns and five rows. In the example on the right, you can see that the three in the top-right 3x3 domain stops there being a three in the middle column of the bottom-right 3x3 domain. This would normally leave open the possibility of the three for that domain being undefined and therefore able to go in either of the two cell marked with the red rectangle. However, the three in the middle cell is in the 't' which extends into the upper half
of the red rectangle therefore meaning that the only cell that three can go in is the
lower of the two.
Without that extra domain, there would be no way of deducing where the seven in the middle
3x3 domain goes. However, whilst the seven in the 3x3 on the right eliminates the middle row,
leaving the cells highlighted with the blue rectangles, there is a seven on the bottom-right
of the 't' that means that a seven cannot go in the 't' anywhere else. In this way, we can
deduce that the only cell a seven will go in is the bottom-left cell.
Click on the puzzle to animate it so illustrate where the 31 domains are. Each 3x3 additional domain is marked as a grey area and has the same rules as the additional domain in the other puzzles. Click here to stop the animation.
Here, like in the Quadrata tutorial, I have marked the letters with numbers and used those
to solve the puzzle where dots are required.
|
Copyright ©2019-2023 Paul Alan Grosse.
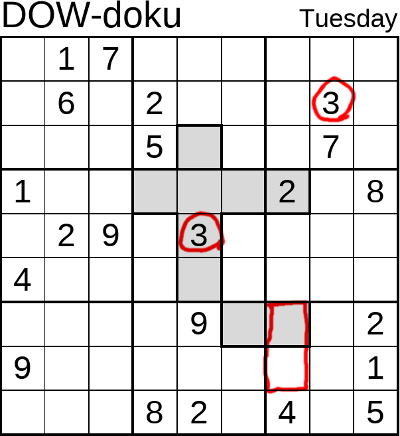 The puzzles with one extra domain in are easy to differentiate from those with four
extra domains in because there are only nine coloured cells in total whereas those with
four extra domains have each domain in contiguous blocks; so, for example, the Motif-doku
puzzle has four distinct, joined-up coloured areas so there is no confusion.
The puzzles with one extra domain in are easy to differentiate from those with four
extra domains in because there are only nine coloured cells in total whereas those with
four extra domains have each domain in contiguous blocks; so, for example, the Motif-doku
puzzle has four distinct, joined-up coloured areas so there is no confusion.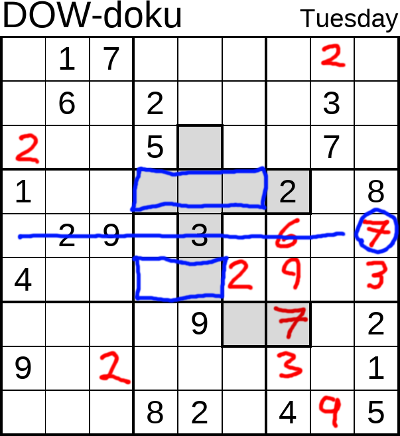 In this example, the three has been written in and therefore the seven ash also been written
in by a process of elimination.
In this example, the three has been written in and therefore the seven ash also been written
in by a process of elimination. This is what the puzzle looks like when it is finished. As you can see, as much of it was
done just by inserting numbers but after a while, I resorted to using dots - see the
tutorials for Kakuro and Quadrata puzzles in case you haven't come across them yet.
This is what the puzzle looks like when it is finished. As you can see, as much of it was
done just by inserting numbers but after a while, I resorted to using dots - see the
tutorials for Kakuro and Quadrata puzzles in case you haven't come across them yet. This is what a Sudoku with an extra four domains looks like. Each additional domain is a
contiguous block, that is to say that there are no odd cells separated from any block as
there are in the single extra domain puzzles.
This is what a Sudoku with an extra four domains looks like. Each additional domain is a
contiguous block, that is to say that there are no odd cells separated from any block as
there are in the single extra domain puzzles. This is the puzzle completed. Again, you can see that I used the spot method to complete it.
You don't have to use spots if you are the sort of person who can memorise all of the data,
it is just that it is sometimes a lot more convenient to use them.
This is the puzzle completed. Again, you can see that I used the spot method to complete it.
You don't have to use spots if you are the sort of person who can memorise all of the data,
it is just that it is sometimes a lot more convenient to use them.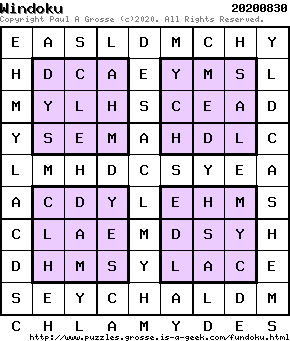 Finally, you can use the solutions from the archive to check the answers to the puzzles.
Finally, you can use the solutions from the archive to check the answers to the puzzles.