Chain-doku Tutorial
|
Chain-doku puzzles are a type of Latin Square - any character cannot appear more than once in each row or column, with an extra constraint that that character also cannot appear more than once in each chain of nine links. In total, there are 27 such domains in a each puzzle, just like a regular Sudoku puzzle except that instead of a 3x3 square, there are nine chains of nine links.
In this section, you are presented with Chain-doku puzzles with numbers and with nine-letter words. You can see from the image on the right - taken from one of the PDF files that you can download of a given day's puzzles - that the 9x9 area has been divided up into sets of chains with nine large links, joined together and laid out so that each of the large, circular links lies in an orthogonal array. This all looks a bit confusing and I can tell you that you have to be very careful when you are
doing the puzzle not to make mistakes. However, if you look at it closely, each chain describes an
area that, whilst it might look the same as a Jigsaw-Doku, actually differs in that the chain can
not only pass over itself but it can also pass over another chain which, whilst it might seem
confusing, does not violate the rule that each chain is separate.
Click on the puzzle to animate it to illustrate the puzzle being solved. the nine 9-link domains are treated the same as the 3x3 domains are in regular Sudoku and you can see that it is solved in the same way. Firstly, the numbers that are on the puzzle already, are marked across and down to eliminate them from cells in columns and rows. Next, they are eliminated from each 9-link domain. Then, a cycle is undertaken of:
Click here to stop the animation. |
Copyright ©2019-2023 Paul Alan Grosse.
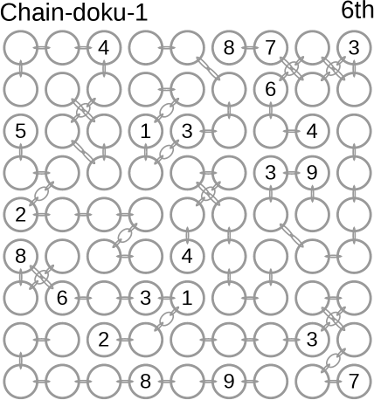 The puzzles that you find almost everywhere, including in the Soduku section of this
site have numbers, although there is a version of each day's puzzle that has alternative
numbers in it so that you do not have a sign that you can readily recognise unless you can
read Gurmukhi numbers.
The puzzles that you find almost everywhere, including in the Soduku section of this
site have numbers, although there is a version of each day's puzzle that has alternative
numbers in it so that you do not have a sign that you can readily recognise unless you can
read Gurmukhi numbers.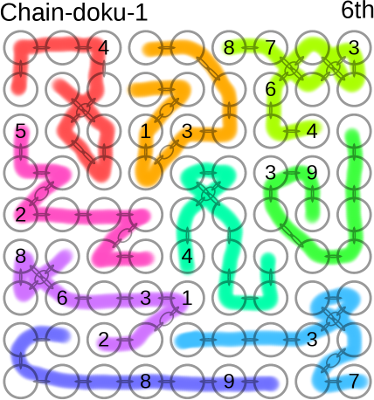 If you print out a puzzle and then get a pack of highlighter pens, you can mark out the domains
that are described by each chain to make it easier to see where they lie. In the image on the right,
that is what has been done.
If you print out a puzzle and then get a pack of highlighter pens, you can mark out the domains
that are described by each chain to make it easier to see where they lie. In the image on the right,
that is what has been done.